Sintonización de un control PID

 El control PID es una de las metodologías más utilizadas en la industria para lograr que un proceso cumpla con los valores requeridos para su correcto funcionamiento y es que, mediante una serie de iteraciones, será posible "forzar" a las variables internas del sistema a tener un valor deseado.

En un artículo anterior revisamos las generalidades de un control PID, conocimos su historia, las partes que lo conforman y dimos un ejemplo de cómo es que cada una de dichas partes afectan el comportamiento y la respuesta del sistema ante distintas entradas. Sin embargo, en esta ocasión realizaremos una revisión más general de cómo realizar la correcta sintonización de un control de este tipo.

Fig. 1: Modelo de control PID.

Variables que interactúan 

Antes de adentrarnos en el proceso de sintonización, debemos conocer qué variables intervienen en el lazo de control, para esto nos apoyaremos en los fundamentos de la teoría de control. Sobra decir que, independientemente de la naturaleza del sistema en cuestión, existen un sinfín de variables que interactúan entre sí para lograr un fin en común, es decir, si nuestro sistema fuese una línea de producción de agua embotellada, para lograr que se complete todo el proceso, habrá variables de naturaleza eléctrica, térmica, hidráulica y neumática en cada una de las distintas etapas de éste, sin embargo, podemos abstraer una serie de definiciones que nos permitirán desarrollar el control para cada variable...en caso de ser necesario.

✔ Variable del Proceso (PV): es aquel valor que se desea controlar, esta variable es intrínseca al sistema y cambiará dependiendo de las necesidades del operador con respecto al proceso.

✔ Set Point (SP o valor prefijado): es el valor que deseamos que tenga la variable del proceso, suele ser la más estable a lo largo del tiempo, es decir, es la que menos cambia de las tres.

✔ Variable de Control (CV): es el valor de la señal que ordena al actuador modificar el estado de la variable de proceso.

Fig. 2: Variables del sistema.

Si bien las variables anteriores son las únicas indispensables, es común el uso de la variable de error que consiste en la diferencia entre el Set Point y la Variable del Proceso, es decir:

Fig. 3: Señal de error.

Sintonización

Curiosamente, no existe hasta la fecha una forma única de realizar una correcta sintonización, no hay un algoritmo que garantice que un valor en específico será el adecuado para que nuestro error converja a cero de forma rápida y sin ocasionar malfuncionamiento de los actuadores, sin embargo, podemos utilizar un método de aproximación que nos permitirá acercar los valores del PID a los requeridos para obtener una respuesta óptima del sistema.

Empecemos revisando la variable del proceso, si esta varía muy rápido lo más recomendado es comenzar con una ganancia proporcional baja, de un valor de 0.1 aproximadamente y una Ki que puede variar entre 1 y 10.

De forma análoga, si la variable del proceso cambia lentamente, podemos comenzar el acercamiento con una ganancia proporcional alta, entre 2 y 8, mientras que Ki deberá ser baja, entre 0.05 y 0.5

Recomendaciones

✔ Ajusta un parámetro a la vez

✔ Observa el efecto de los ajustes antes de realizar cambios adicionales

✔ Inicia con un control puramente proporcional para evitar daños en los actuadores

✔ Si la primera aproximación proporcional no es suficiente, intenta duplicando su valor

✔ Cuando el sistema comience a oscilar, reduce la ganancia proporcional a la mitad

✔ Añade una ganancia integral pequeña

✔ Duplica el valor integral hasta que el sistema comience a oscilar, en ese momento, reduce su valor a la mitad

✔ Esto te acercará bastante a los valores reales del PID que pueden ser logrados con ajuste fino

Ejemplo

Para ejemplificar esta explicación utilizaremos Matlab, debido a que nos ofrece la posibilidad de analizar una planta sin contar con ella físicamente:

Fig. 4: Modelo de planta en lazo cerrado.

Comenzamos analizando la respuesta sin efecto del control PID, donde podemos observar que la variable del proceso cambia muy lentamente, esto nos indica que la primera aproximación deberá ser con una ganancia proporcional grande.

Fig. 5: Respuesta natural del sistema.

La primera aproximación la hacemos con un control puramente proporcional con una magnitud de 5, esto nos entrega la siguiente respuesta en donde observamos que la banda de error entre el set point y la variable del proceso se reduce, sin embargo, como aún es muy grande, podemos aumentar el valor del controlador.

Fig. 6: Control proporcional.

El segundo acercamiento lo hacemos con un valor de 10, esto permite reducir aún más la banda de error:

Fig. 7: Respuesta del sistema para P=10.

Esta ganancia se siguió aumentando hasta un valor de 40, donde podemos observar que aparecen oscilaciones de magnitud considerable, este valor será la referencia y, como indica el método, deberá ser reducida a la mitad. Es decir que el valor proporcional se reduce a 20, esto nos entrega la siguiente respuesta:

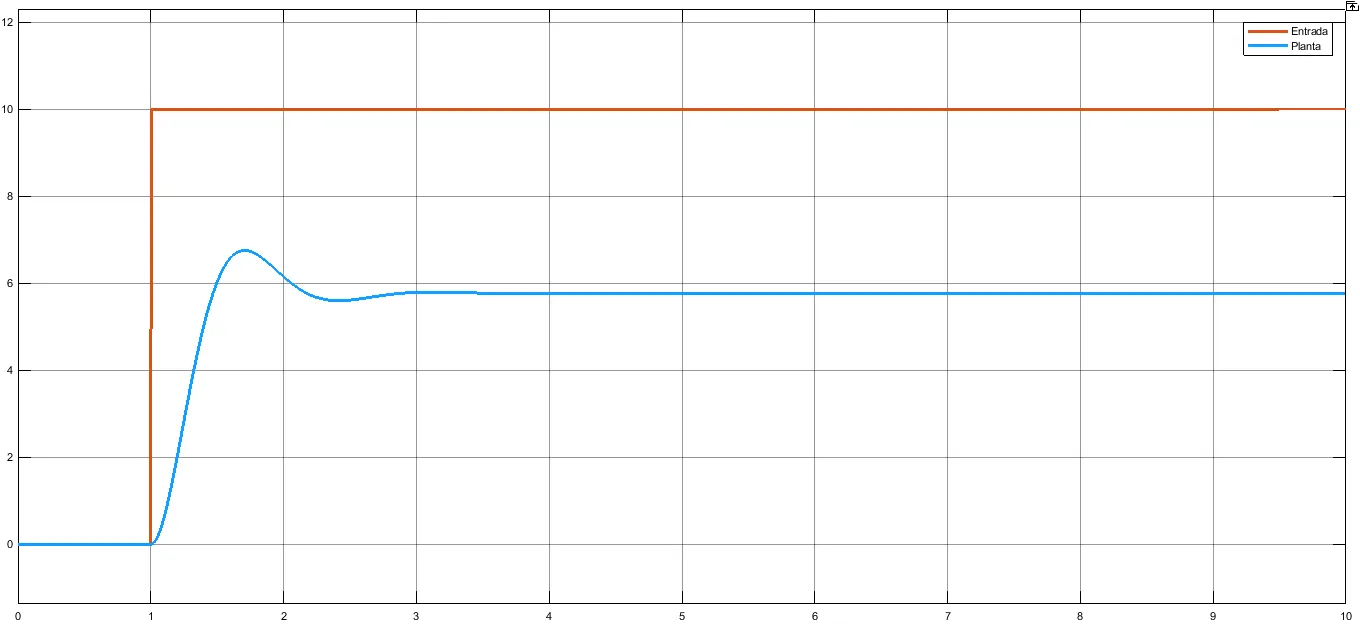Fig. 8: Respuesta del sistema para P=20.

Observamos que aún existe una banda de error, sin embargo, en lugar de aumentar la ganancia proporcional, es momento de introducir la ganancia integral con un valor de 0.5:

Fig. 9: Respuesta del sistema con un control PI.

Observamos que el efecto de la ganancia integral es "forzar" la respuesta del sistema a alcanzar el valor deseado (Set point). Continuamos aumentando el valor de I hasta obtener una respuesta que sea adecuada a nuestras necesidades, en este caso, una respuesta rápida:

Fig. 10: Respuesta para P = 20 e I = 2.

Si bien la respuesta es adecuada, podemos realizar un ajuste fino con tal de reducir el sobrepaso de la respuesta, lo cual permitirá una curva más suave que significará un menor esfuerzo en los actuadores, prolongando su vida útil y reduciendo costos de mantenimiento. El valor final de nuestro controlador es P = 16 e I = 2:

Fig. 11: Respuesta final del sistema.

¿Qué pasa con la ganancia derivativa?

Te habrás dedo cuenta que en los ajustes mencionados en este artículo se enfocan únicamente en las ganancias proporcionales e integrales, dejando de lado la derivativa, pero, ¿a qué se debe esto? Dado el modelo matemático del control PID, la ganancia proporcional representa una acción predictiva, es decir, permitirá a nuestro control hacer los ajustes necesarios con el fin de reducir las perturbaciones presentes en la variable del proceso.

Fig. 12: Definición de la ganancia derivativa.

Es decir, su valor significa qué tanto tiempo en el futuro será posible predecir la tasa de cambio de la variable del proceso, por lo tanto, este parámetro permite crear una respuesta más rápida en el lazo de control que también significará una mejor desempeño del control. Sin embargo, debido a que el parámetro derivativo mide el cambio en el tiempo de PV, será necesario que dicha variable sea una señal limpia, sin perturbaciones ni ruido de ningún tipo.

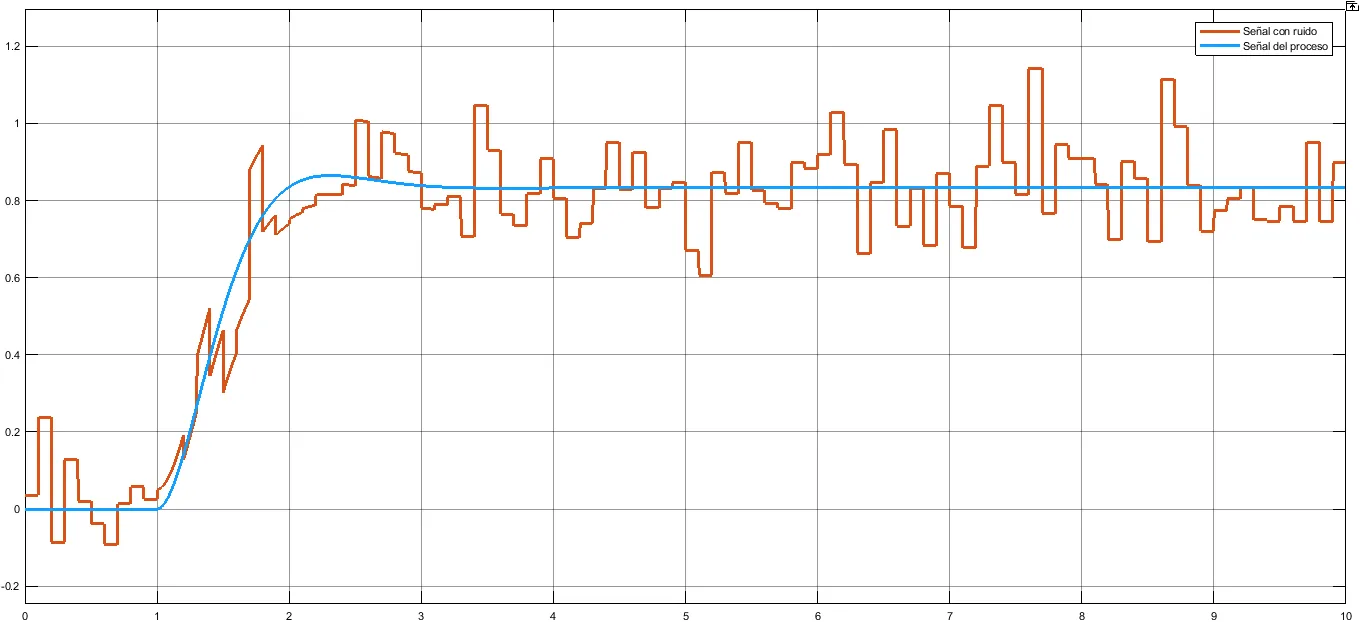Fig. 13: Variable del proceso con ruido vs señal limpia.

Esto último resulta sumamente complicado pues, en un entorno industrial, la gran cantidad de equipos eléctricos, electrónicos, electromagnéticos e incluso mecánicos; su cercanía e interacción, ocasionarán que la variable del proceso se vea afectada y si bien es posible desarrollar filtros electrónicos, al desconocer el valor real de VP, sería prácticamente imposible encontrar qué frecuencia debe ser eliminada de la señal en cuestión.

Debido a esto, el control derivativo suele ser el menos utilizado de las posibles combinaciones del PID. Siendo el más común el control PI (como ya vimos en este artículo), el control proporcional puro P y el control PID completo son usados de forma ocasional dependiendo de la naturaleza del proceso y, como es de esperarse, el control PD es el menos utilizado.

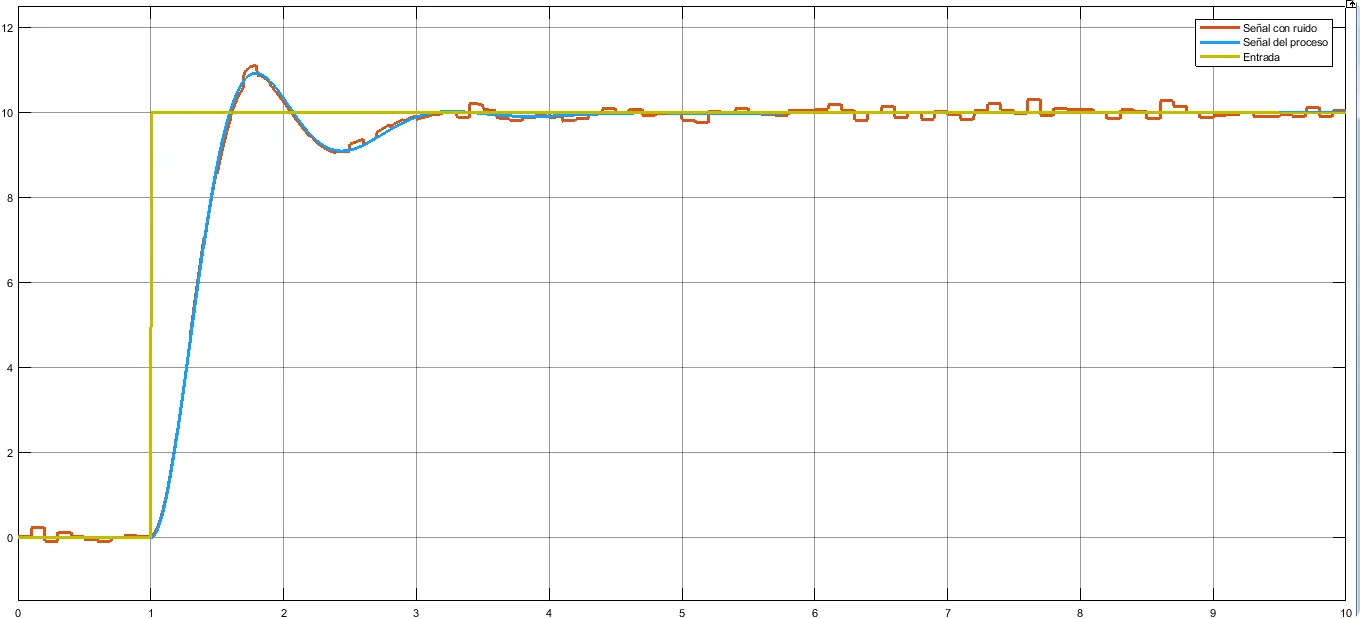Fig. 13: Control PI en señal con ruido vs señal limpia.

Conclusiones

Parecería que el control PID es ventajoso y desventajoso al mismo tiempo, sabemos que existen un gran número de motivos por los que es el más recurrido a nivel industrial, sin embargo, no es la solución definitiva en todos los procesos del sector. Esto último no debería de ser sorpresa pues, como hemos visto en un gran número de artículos de este sitio, la industria es tan diversa que es imposible concebir una tecnología o una metodología única que aplique a todos y cada uno de los distintos procesos que la componen.

Respecto a la sintonización del control, el acercamiento aquí mostrado es el resultado de dos corrientes de estudio. En primer lugar, tenemos el fundamento teórico de donde nace la ecuación del control PID que ya todos conocemos y, por otra parte, el estudio empírico o de campo, donde, a partir de la observación del comportamiento ante distintos valores de las constantes PID, se alcanza una respuesta óptima con acercamientos conservadores que no ponen en riesgo a los equipos de campo.

Al final, todo recae en qué tipo de proceso deseamos controlar, en la naturaleza de las variables y qué tipo de respuesta necesitemos del proceso.

¿Te gusta nuestro contenido? Lee nuestros otros artículos, comparte este artículo con alguien a quien le resulte útil y considera apoyarnos con una donación mediante paypal en este enlace.

¿Tienes dudas, comentarios o sugerencias? Utiliza la sección al final de esta página o contáctanos en nuestras redes sociales.

Igual que siempre, gracias por leer.

-AHN