Cálculos eléctricos básicos (parte 2)

Continuando con la serie dedicada a cálculos eléctricos, dedicamos esta segunda parte a lo referente a corriente alterna cuya naturaleza es muy distinta a la corriente directa y su utilización conlleva distintas consideraciones en lo que respecta a su comportamiento y los cálculos que se aplican.

En esta ocasión nos centraremos en cuestiones básicas como son el cálculo de impedancia mediante resistencia y reactancias. También revisaremos las modificaciones aplicadas a la ley de Ohm simple para obtener voltajes y corrientes, además de una revisión sobre los tipos de potencia que estos circuitos manejan.

▶ Impedancia ◀

Como anticipamos anteriormente, existen variantes de las ecuaciones previas al tratarse de corriente alterna pues ya no solo encontraremos resistencias como elementos de carga, sino que aparecerán otros como son inductores y capacitores, haciendo que el la carga tome el nombre de impedancia que se compone de los siguientes elementos:

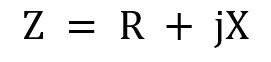Ec. 1: Impedancia compleja.

Donde R es la parte resistiva, j es la referente al conjunto complejo de los número y X es la conjunción de inductancia y capacitancia que se calcula de la siguiente forma, donde f es la frecuencia de la corriente alterna, C la capacitancia y L la inductancia:

Ec. 2: Cálculo de reactancias

Y si deseamos hacer un cambio en el dominio de los complejos al de ángulos, utilizamos la propiedad trigonométrica de la tangente inversa:

Ec. 3: Conversión de número complejo

Pues de esta forma se facilitaría el cálculo de corriente y tensiones.

▶ Voltajes ◀

Ahora, en lo que concierne al voltaje, también encontramos distintas variantes que provienen de la naturaleza oscilante de este tipo de corriente. Comenzamos con el voltaje pico-pico que es la amplitud de la onda de voltaje:

Fig. 1: Voltaje en corriente alterna

Y, en consecuencia, el voltaje pico es la mitad de la onda:

Ec. 4: Voltaje pico

Aquí entra el concepto más importante que es el valor de voltaje eficaz (también llamado RMS) cuyo significado es: un valor en corriente directa que realizará los mismos efectos que un valor en corriente alterna a una resistencia en Ohms. Este valor se calcula de con la siguiente ecuación, pues tratamos con onda de tipo sinusoidal:

Ec. 5: Cálculo de voltaje eficaz (o RMS)

▶ Ley de Ohm ◀

Respecto al cálculo de la corriente, en este caso se conserva la ley de Ohm, variando únicamente en el tipo de voltaje utilizado y que nuestra resistencia ahora es una impedancia completa, esto conlleva a que se tenga una componente compleja producto de la reactancia del circuito:

Ec. 6: Ley de Ohm en corriente alterna.

▶ Potencias ◀

Respecto al cálculo de potencias, nuevamente encontramos distintos tipos. Comenzamos el análisis con la potencia activa que es aquella que se transforma en energía útil, es decir, aquella que se transforma en calor o trabajo. Ésta se mide en watts [W]:

Ec. 7: Potencia activa

Dato: El coseno del ángulo fi se conoce como factor de potencia y se puede calcular de la siguiente forma:

Ec. 8: Factor de potencia

Después encontramos la potencia reactiva, la cual representa la energía consumida por los inductores y capacitores del circuito. Ésta se mide en Volts-Ampere Reactivos [VAR]:

Ec. 9: Potencia reactiva

Finalmente, realizando una suma vectorial de las anteriores, encontramos la potencia aparente. Se mide en Volts-Ampere [VA] y se calcula con la siguiente ecuación:

Ec. 10: Potencia aparente

▶ Solución a un circuito RLC ◀

Podemos proponer el siguiente circuito, donde la fuente de alimentación es de 340[Vpp] a 60 [Hz], esto nos permite calcular el voltaje RMS:

Fig. 2: Circuito RLC en serie

Ec. 11: Cálculo de voltaje RMS.

Ahora procedemos a calcular el valor de las reactancias y la impedancia total con las ecuaciones mencionadas al inicio de este artículo:

Ec. 12: Cálculo de reactancias

Ec. 13: Cálculo de impedancia total

Considerando que necesitaremos el factor de potencia más adelante y el valor del ángulo φ podemos calcular a partir de la expresión correspondiente, sin embargo, es necesario calcular antes el módulo de la impedancia:

Ec. 14: Cálculo de factor de potencia

Ahora encontramos la corriente con la ley de Ohm:

Ec. 15: Cálculo de corriente eficaz.

Y finalmente procedemos a calcular las potencias correspondientes a este circuito en corriente alterna:

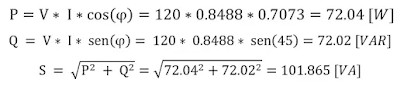Ec. 16: Cálculo de potencias.

▶ Conclusiones ◀

Si bien el uso de corriente alterna representa un grado más alto de complejidad en comparación con los circuitos de corriente directa, podemos observar que las propiedades básicas se conservan pues, como podemos obtener un valor de tensión, corriente o impedancia aplicando la ley de Ohm.

También es posible utilizar la ley de Watt para las potencias pues aunque encontramos tres tipos, los primeros dos cumplen el mismo modelo matemático y el último (la potencia aparente) es solo un modulo vectorial de las anteriores.

Esta es solo la segunda parte de la serie dedicada a cálculos básicos generales (visita la primera haciendo click en este enlace) , en posteriores artículos veremos aplicaciones a otros equipos como son motores, transformadores, líneas competas, etc. 

¿Tienes dudas, comentarios o sugerencias? Contáctanos en la sección de comentarios o a través de nuestras redes sociales, recuerda que siempre estamos abiertos a sugerencias sobre qué temas desarrollar.

¿Te gusta nuestro contenido y quieres apoyarnos? Considera una donación mediante paypal en este enlace.

Y como siempre, gracias por leer.

-AHN